Dor Abrahamson
|
 |
Embodied Design: Developing a Research Program
Embodied design is a framework for innovating educational products. More specifically, it is a theoretically informed pedagogical framework that both nurtures, and is nurtured from, the design-research practice of developing, evaluating, and modeling instructional resources and facilitation guidelines. This practice serves as a context for scholars to identify and pursue research problems germane to the learning sciences, because task-oriented activities that surface students’ core cognitive challenges in understanding target concepts often create empirical opportunities to hone enduring research problems. In his talk, Abrahamson will set the scene for the symposium by outlining the inspirations of embodied design and its activity genres, which are perception-based and action-based. Looking in particular at action-based embodied design, Abrahamson will demonstrate how studies incorporating the Mathematics Imagery Trainer, which have drawn on new technology for multimodal interaction as well as methodological instruments for data gathering, analysis, and visualization, are creating for researchers opportunities to ask and attempt to answer ‘big’ questions regarding the cognitive and sociocultural constitution of mathematical understanding.
Shakila Shayan, Marieke van der Schaaf, Arthur Bakker and Rosa Alberto, Utrecht University, Netherlands.
Embodied design for proportional reasoning
Building on the embodied design research by Abrahamson and colleagues on proportional reasoning, we have used eye-tracking technology to study how students solve tasks in variants of the original mathematical imagery trainer for proportion (MIT-P), a multi-touch table application. In MIT-P the task for students is to make a screen green. This is only the case if their hands are positioned at a particular proportion on the screen (say 1:2). Students then learn to keep the screen while moving both hands proportionally in one, vertical dimension. Our extended version (MIT-Ext) includes two-dimensional variants with and without guidance. We report on findings from a succession of empirical studies with over 120 students in primary and prevocational education. We compare results from one-dimensional versus two-dimensional representations, and results from variants in which students’ attention is guided by a rectangular shape. A topic of particular concern is students’ attentional anchors on places that are mathematically relevant. The data so far seem to suggest that guidance by means of the rectangular shape prevent students from constructing mathematically relevant attentional anchors themselves. All variants of the embodied design of proportional reasoning seem to have particular pedagogical pay-offs.
Designs
 MIT-Ext includes various extensions based on MIT-P
MIT-Ext includes various extensions based on MIT-P
Results

Typical gaze patterns during the interaction with MIT-Ext variants.
 |
|
Guided Enactment: Designing Visual Cues for Sensorimotor Engagement
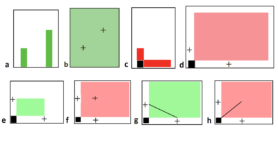
The purpose of this short demonstration is to present a new embodied-design principle that utilizes “cuing”: steering students’ visual attention towards target locations as they learn with interactive platforms. The working hypothesis is that when students engage in learning with interactive platforms, certain visual cues could enhance learning of target mathematical concepts by eliciting target sensorimotor schemes. I will present a software application (“app”) that is based on Abrahamson’s Mathematical Imagery Trainer genre. The app carries the objective of steering the user to develop particular sensorimotor orientations toward manipulating the vertices of a virtual rectangle; each cue aims to foster sensorimotor grounding of a different mathematical concept (see figure 1). In addition, I will propose an elaboration of the cuing principle to other mathematical concepts related to the properties of quadrilaterals.
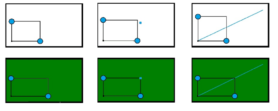 Figure1: Interactive tablet application. The screen will be green for all rectangles of an unknown aspect ratio, here 1:2. Top row shows three initial interface displays corresponding to different cues; below each image is a solution in relation to this cue. a. No cue; b. Leading Point cue for the target location of the top-right rectangle vertex; and c. Diagonal Line cue, the axis for all “green” locations of the top-right vertex. The bottom-left vertex of the rectangle is fixed. Students are asked to use their Left-hand and Right-hand index fingers to move the rectangle’s blue vertices so that the screen becomes green and then remains green as they keep moving their hands.
Figure1: Interactive tablet application. The screen will be green for all rectangles of an unknown aspect ratio, here 1:2. Top row shows three initial interface displays corresponding to different cues; below each image is a solution in relation to this cue. a. No cue; b. Leading Point cue for the target location of the top-right rectangle vertex; and c. Diagonal Line cue, the axis for all “green” locations of the top-right vertex. The bottom-left vertex of the rectangle is fixed. Students are asked to use their Left-hand and Right-hand index fingers to move the rectangle’s blue vertices so that the screen becomes green and then remains green as they keep moving their hands.
Daniela Schansker, Angelika Bikner-Ahsbahs
|
 |
A scaffolding step: Haptic actions integrated into a technology-based embodied design
In a design-based research study on the extension of the decimal place value system from natural to decimal numbers we are examining the learning processes of grade 5 students working with a digital place value chart (DPC) on the iPad. In this chart, dragging one token to the neighboring column on the right (e.g. from tens to ones; proximal movement) provokes the emergence of ten tokens out of the dragged token on the screen (distal movement). This way de-bundling one ones into ten tenths can be expressed by a pair of proximal and distal movements. The latter is the core step of extending the DPC from natural to decimal numbers. Data analyses in our empirical study have shown, that the use of just the DPC does not provide students with experience to execute this core step in a mathematically meaningful way. They just tend to refer to de-bundling in terms of dragging in speech and gestures. There is no indication of how the exchange of one ones by ten tenths can be thought of, for example with respect to the concept of fractions as partitioning into ten equal parts. In our talk, we will present a scaffolding design and its empirical investigation to integrate haptic actions into the students’ interaction with the DPC, following two principles: (1) modelling the 2D-tokens as projections of 3D-towers and (2) providing material 3D-towers for their haptic partitioning into ten equal parts. Our data analysis shows that the partitioning idea of this scaffolding design is integrated into the concept of de-bundling as an add-on-meaning that allows the extension from natural numbers to decimal fraction preserving the principles of the digital place value system.

Michiel Veldhuis & Marja van den Heuvel-Panhuizen
|
 |
The role of embodiment in developing higher-order mathematical thinking in primary education
We present first results of three educational experiments aimed at fostering higher-order thinking in mathematics in primary school by making use of embodiment. While, internationally, awareness is increasing that the foundation of mathematical higher-order thinking should be laid at a young age, in the Dutch primary school curriculum higher-order thinking is almost absent. To provide evidence for ways of making the current ‘flat’ mathematics curriculum more mathematical, the ‘Beyond Flatland’ project is investigating, in three experimental studies in fifth-grade classes, what opportunities-to-learn higher-order thinking can be offered regarding the content domains of (i) early algebra, (ii) dynamic data modeling, and (iii) probability. With these studies we aim to contribute to understanding the role of embodied experiences in developing domain-specific higher-order thinking in primary mathematics education. In this presentation, we provide snapshots of the designed tasks and activities in the three content domains, and discuss resulting student reasoning.
 |
 |
 |
 |
Dragan Trninic
|
Restoring the Historical Role of Practice to Mathematics Education
This talk concerns a particular interpretation of Freudenthal’s claim that mathematics should be taught like swimming (i.e., like a physical discipline). The argument being made is that “direct instruction” and “discovery” are not opposite but complementary, linked by repetitive yet explorative practice. This claim is elaborated through an empirical case of martial arts instruction. That repetitive practice can nonetheless be a fountainhead of discovery is explained using Bernstein’s notion of repetition-without-repetition and Vygotsky’s notion of kinesthetic sensations. Finally, we attend to parallels in canonical mathematics practice, with a focus on reconceptualizing direct instruction, repetition, and discovery as complementary and synergistic.
Ami Shulman
|
 |
Embodiment — the field of connective potentials. An Introduction to the Feldenkrais Method
This short introduction to the Feldenkrais Method – a comprehensive integrative movement system that correlates thought with action – elicits a felt sense of embodiment that lies at the potential of not only all movement possibilities but also of all cognitive possibilities, including mathematical reasoning.
Anna Shvarts
|
 |
Coordination versus dis-coordination in student-tutor collaboration during an embodied activity.
Vygotsky stresses the importance of collaboration between a child and an adult for cultural development. The detailed analysis of the interaction between a student and a tutor, while they are engaged with embodied computer-based mathematical task discloses the micro-mechanisms by which the cultural meaning emerge in the student’s consciousness. In this research, we analyzed the student –tutor collaboration on the embodied task on parabola definition by means of dual eye-tracking. The period of strong synchronous coordination between sensory-motor systems of the participants was superseded by dis-coordination of the students’ and the tutors’ perceptual strategies. At this stage, the tutors’ eye-movements evidenced the attentional anchors of enculturated mathematical perception earlier than these attentional anchors emerged in the students’ perception. We assume that this dis-coordination suited the purpose of tracking the efficiency of the students’ embodied activity in order to distinguish the right moment for a teaching intervention. The research exemplifies how dual eye-tracking methodology may enhance microanalysis of student-tutor collaboration and may reveal new insights about teacher’s tactics.

Maike Schindler
|
 |
Interpretation of single and dual eye-tracking data in natural settings
Eye-tracking helps us to get closer to students’ problem-solving processes in mathematics. However, even in suitably visually presented tasks, interpretation of eye-tracking data is non-trivial. A key reason is that the interpretation of eye-tracking data is context-sensitive and entails certain ambiguity and uncertainty. In the talk, I will address the questions of how eye-tracking data can be interpreted and what inferences can be made. I will discuss opportunities and potential limitations that eye-tracking data analysis entails. In particular, I will address eye-tracking with glasses, which allows students to work in natural settings that they are familiar with. I will present empirical studies in which single students worked on mathematical problems (“portable single eye-tracking”) as well as a study in which two students worked collaboratively on mathematical problems wearing eye-tracking glasses (“portable dual eye-tracking”).


